separators

www.thecementgrindingoffice.com

Separators in the cement industry

Cyclones

2.1

Introduction:

In cement manufacturing industries, large-sized cyclone separators are used as main process equipments in

significant numbers for handling high volumetric flow rates of dust-laden gases.

The cyclone is a simple mechanical device commonly used in the grinding circuits to remove relatively large particles

from gas streams.

Cyclones are often used as precleaners to remove more than 80% of the particles greater than 20µm in diameter.

Smaller particles that escape the cyclones can then be collected by more efficient control equipment like bag filters

and electroprecipitators.

Cyclones are relatively inexpensive since they have no moving parts and they are easy to operate.

The most common type of cyclone is known as reverse flow cyclone separator.

2.2

Advantages of cyclones:

Low capital cost.

Ability to operate at high temperatures and pressures.

Low maintenance requirements because no moving parts.

Constant pressure drop.

Can separate both solid and liquid particles, sometimes both simultaneously.

2.3

Disadvantages of cyclones:

Low efficiency especially for very small particles.

High operating costs in case of high pressure drop.

Subject to erosion or clogging if abrasive solids are processed.

2.4

Principle of operation:

The spiral pattern of gas flow is developed by the manner in

which the gas is introduced.

It enters along the side of the cyclone body wall and turns a

number of times to spiral down (external vortex) to the

bottom.

Particles in the gas are subjected to centrifugal forces which

move them radially outwards, against the inward flow of gas

and towards the inside surface of the cyclone.

When the gas reaches the bottom of the cyclone, it reverses

direction and flows up the center of the tube, also in a spiral

fashion.

This spiral fashion is also called inner vortex and fine

particles are carried with the air and leave the cyclone

through the immersion tube.

Solids at the wall are pushed downwards by the outer vortex

and are going out by the solids exit.

Gravity has been shown to have little effect on the

cyclone's operation.

See the figures on the right side and below.

Click on the picture to enlarge

www.thecementgrindingoffice.com

2.5

Forces affecting the particles

We consider a reverse flow cyclone with a cylindrical section of radius R.

Particles entering the cyclone with the gas stream are forced into a circular motion.

The forces acting on a particle following a circular path are drag, buoyancy and centrifugal force (Fd, Fb and Fc).

The balance between these forces determines the equilibrium orbit adopted by the particle.

The drag force is caused by the inward flow of gas and acts radially inwards.

Considering a particle of diameter x and density ρp following an orbit of radius r in a gas of density ρf and viscosity µ,

we have the tangential velocity of the particle be Uϴ and the radial inward velocity of the gas be Ur.

If we assume that the Stokes’ law applies under these conditions then the drag force is given by:

The centrifugal and buoyancy forces acting on the particle moving with a tangential velocity component Uϴ at radius r are:

We can neglect the buoyancy force.

And at a steady state, we have:

Click on the picture to enlarge

2.6

Flow Characteristics

The rotational flow in the forced vortex within the cyclone body gives rise to a radial pressure gradient.

This pressure gradient, combined with the frictional pressure losses at the gas inlet and outlet and losses due to changes in flow

direction, make up the total pressure drop.

The pressure drop, measured between the inlet and gas outlet, is usually proportional to the square of gas flow rate through

the cyclone.

A resistance coefficient, the Euler number Eu, relates the cyclone pressure drop Δp to a characteristic velocity:

Where ρf is the gas density

The velocity v is based on the cross-section of the cylindrical body of the cyclone:

Where Q is the gas flow rate and D is the cyclone inside diameter

The Euler number represents the ratio of pressure forces to the inertial forces acting on a fluid element.

Value is practically constant for a given cyclone geometry, independent of the cyclone body diameter.

www.thecementgrindingoffice.com

2.7

Mechanical parts:

Tangential inlet volute

Cylindrical section

Immersion tube

Conical section

Discharge (rotary valve, pendulum flap)

2.8

Cyclones families:

Conventional

High efficiency

High capacity

See the figure on the right:

Click on the picture to enlarge

2.9

Design of the cyclones:

Dimensions:

a = Height of tangential inlet

b = Width of tangential inlet

De = Diameter of air outlet tube

S = Immersion length of outlet tube

D = Cyclone diameter

h = Length of cylindrical section

z = Length of conical section

H = Cyclone length

B = Diameter of material outlet

Click on the picture to enlarge

On the sheet below, we can have a good idea of the standard cyclone dimensions for each family:

Regardless of the configuration selected, we must follow the following recommendations:

* a ≤ S to avoid the by-pass of the particules from the input section directly to the tube exit

* b ≤ (D-De)/2 to avoid an excessive pressure drop

* H ≥ 3D to keep the tip of the vortex formed by the gases inside the conical section of the cyclone

* The inclination angle of the cone of the cyclone should be ≈ 7-8° to ensure a quick slide of the powder

* De/D ≈ 0,4-0,5, H/De ≈ 8-10 and s/De ≈ 1 to ensure the operation with the maximum efficiency

www.thecementgrindingoffice.com

2.10

Cyclones scale-up:

The scale-up of cyclones is based on a dimensionless parameter, the Stokes number, which characterizes the separation

performance of a family of geometrically similar cyclones.

The Stokes number (Stk50) is deﬁned as:

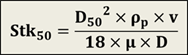
It is interesting to find that, for well-designed and well-known cyclones, there is a direct correlation between Eu and Stk50:

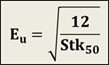
For Stairmand high-efficiency cyclones: Stk50 = 1,4/10000 and Eu = 320

For Stairmand high-capacity cyclones: Stk50 = 6/1000 and Eu = 46

2.11

Cyclone's efficiency:

A model widely accepted is use for determining the efficiency of a cyclone.

In this model, Ne is the number of revolutions the gas falling in the outer vortex.

The equation is:

See the "Design of cyclones" section to know the parameters.

With the model of Lapple (1951) which is an empirical relationship in order to calculate the cut size (50% of efficiency),

we have:

Where:

Vi is gas inlet velocity in m/h (range in m/sec: 15-30 m/sec) and

µ is the air viscosity in kg/m.h

b is the width of the tangential inlet in m

ρp is the solid density in kg/m3

ρf is the air density in kg/m3

The efficiency (Ƞi) of any size of particle is given by the following formula:

Where Di is the particle of reference of a range

The overall efficiency of the cyclone is a weighted average of the collection efficiencies for the various size ranges and is

given by:

Where mi is the mass of particles in a certain range and

M is the total mass of particles

This efficiency can be undervalued with the concentration of solid particles in the air flow rate.

Then, when the concentration is higher than 2 gr/m3, a correction is applied:

where Ƞ1 is the efficiency found,

C1 is 2 (gr/m3),

Ƞ2 is the new efficiency and

C2 is the concentration in dust

www.thecementgrindingoffice.com

2.12

Cyclone's pressure drop:

In the evaluation of a cyclone design, pressure drop is a primary consideration. Because it is directly proportional to the

energy requirement, under any circumstance, knowledge of pressure drop through a cyclone is essential in designing

a fan system.

Many models have been developed to determine the cyclone pressure drop but one of the well accepted is the model

of Shepherd and Lapple (1939).

The formula of Δp is:

K is a constant:

K = 16 for tangential inlet without neutral inlet vane

K = 7,5 if tangential inlet with neutral inlet vane and large cyclones

It is better to keep a pressure drop lower than 2,5 kPa.

2.13

Design modifications and consequences:

2.14

General methodology for the design of cyclones

1. Select a configuration (conventional, high efficiency or high capacity)

2. Select a speed at inlet (15-30 m/sec)

3. In function of the flow rate importance, it is useful to have a 1st estimation of the cyclones number

4. Calculate the diameter of the cylindrical section of the cyclone D

5. Calculate the other dimensions of the cyclone on the basis of the table for the selected configuration

6. Calculate the pressure drop

7. To analyze if D and Δp are excessively large. Analyze the possibility of using various cyclones in parallel.

For nc cyclones in parallel repeat items 2 and 3 using the value of Q/nc in place

8. Calculate efficiencies for fractions and the total

9. Compare the calculated efficiency with desired. If you do not achieve the desired value, use a larger value of speed inlet

10. Estimate the cost of the cyclone

An example of cyclone calculation is presented on the following page.

www.thecementgrindingoffice.com

SpreadsheetConverter

The fields with the red border are required.